本文以英文撰写。中文版由 DeepSeek 翻译。原文请参阅 英文版。

形式系统的组成

• 公理：被视为理所当然的基本假设。
• 推理规则：允许我们从公理中推导出新定理的规则。
• 定理：通过推理规则从公理中推导出的陈述。
• 证明：使用推理规则从公理中推导定理的过程。
• 一致性：如果无法从公理中推导出矛盾，则形式系统是一致的。
• 完备性：如果每个真陈述都可以在系统中被证明，则形式系统是完备的。
• 可判定性：如果存在一个算法可以确定给定陈述是否是系统的定理，则形式系统是可判定的。

以MU谜题为例。

• 公理：MI
• 推理规则：
  1. 如果定理的最后一个字母是$I$，则可以在末尾添加一个$U$。
  2. 如果$Mx$是一个定理，则$Mxx$是一个定理。
  3. 如果$III$出现在定理中，则可以替换为$U$。
  4. 如果$UU$出现在定理中，则可以删除。
• 证明：证明$MIIU$是一个定理。
  • $MII$（从$MI$使用第一个推理规则）
  • $MIIII$（从$MII$使用第二个推理规则）
  • $MIIU$（从$MIIII$使用第三个推理规则）

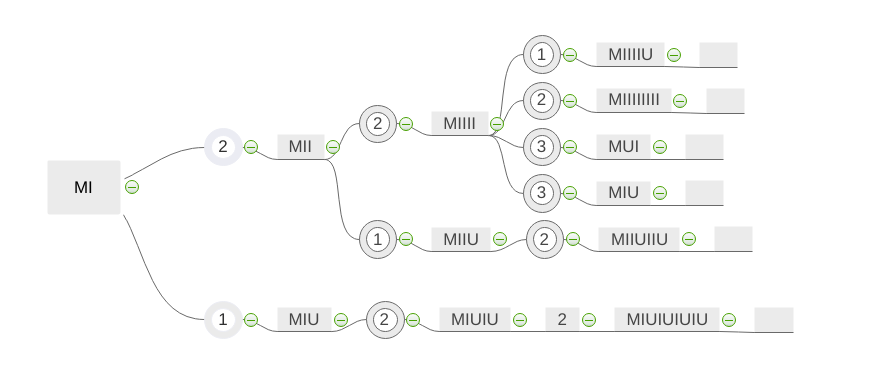
值得注意的是，中文版的MU谜题使用了“WJU”三个字母，而不是“MIU”。我将在后面的部分解释原因。

$MU$是一个定理吗？

很明显，MU谜题中的所有定理都具有$Mx$的形式，其中$x$是由$I$和$U$组成的字符串。原因是，没有任何推理规则可以在定理中添加$M$或移除$M$。

这个结论基于对MU谜题中定理结构的观察。我们将这种推理称为跳出系统的推理。

然而，我们仍然无法确定$MU$是否是一个定理。我们可以尝试列出MU谜题中的所有定理，并检查$MU$是否在列表中。但这不是一个可行的解决方案，因为定理的数量随着字符串的长度呈指数增长。用更专业的术语来说，我们无法在有限的时间内确定$MU$是否是一个定理。

自底向上与自顶向下

自底向上：从公理开始，使用推理规则推导定理。

自顶向下：从定理开始，尝试找到可以推导它们的公理。

上一节是自底向上方法的一个例子。自顶向下方法更困难。

我们使用$pq$形式系统来说明自顶向下方法。$pq$形式系统的公理是：

• 公理：$x-qxp-$，其中$x$是由$-$组成的任何字符串。
• 推理规则：如果$xqypz$是一个定理，则$x-qypz-$是一个定理。

唯一的推理规则表明，当$x$加一时，$z$也必须加一。

很容易看出，$pq$形式系统的定理具有$xqypz$的形式，并且必须满足$x=y+z$。

因此，当我们想确定一个字符串是否是$pq$形式系统的定理时，我们只需检查短横线的数量是否满足定理的要求。

例如，$----q--p--$是$pq$形式系统的一个定理，因为$4=2+2$。

这种推理被称为自顶向下方法。

M模式、I模式和U模式

MU谜题以鼓励在MIU系统中进行一定程度的探索的方式提出。但它也以一种不暗示停留在系统内必然会有所收获的方式提出。

MU谜题中有三种思维模式：

• 机械模式：在这种模式下，你机械地遵循系统的规则。你只需逐个写下使用推理规则从公理中推导出的所有定理。
• 智能模式：在这种模式下，你试图理解系统中定理的结构。你试图看看是否有模式或规则支配着这些定理。
• 无模式：一种禅宗式的问题处理方法。

这就是为什么中文版的MU谜题使用“WJU”三个字母而不是“MIU”。“W”代表“惟”，在中文中意为“从心”，“J”代表“机”，意为“机械”，“U”代表“无”，意为“无”。

同构诱导意义

我们已经创建了两个形式系统“WIU”和“pq”系统，然而，这两个系统没有明显的“意义”。

我们需要在形式系统和现实世界之间创建一种映射，以赋予系统意义。这被称为同构。

例如，“pq”系统可以映射为两个数字的加法。
$\begin{aligned} q &\iff =\\ p &\iff +\\ - &\iff 1\\ -- &\iff 2\\ --- &\iff 3\\ &\vdots \end{aligned}$

同构并不唯一。我们也可以将“pq”系统映射为两个数字的减法。

算术的失常

pq系统为我们提供了一种表示两个数字加法的方式。让我们更多地思考数字系统。

人们喜欢发明违反基本算术但说明“更深”真理的口号，例如“1+1=1（对于恋人）”，或“1+1+1=1（三位一体）”… 两滴雨滴在窗玻璃上合并；一朵云分裂成两朵云。如果你思考这个问题，你可能会提出一些涉及物体在空间中分离的标准，并确保每个物体都能清楚地与其他物体区分开来。

数字作为现实会失常。然而，人们有一种古老而天生的感觉，认为数字不应该失常。

解放，M.C. Escher

数字的一种失常可能是无限序列。以欧几里得定理为例，该定理指出存在无限多个质数。

该定理的证明是告诉人们，无论你选择的数字有多大，总有一个更大的质数。让我们选择数字$N$。我们可以构造一个新数字$N!+1$。这个新数字不能被从$2$到$N$的任何数字整除。换句话说，$N!+1$只能被比$N$大的数字整除。所以它本身要么是质数，要么其质因式分解的数字大于$N$。

我们绕过无限的方式是使用“潜在无限”的概念。我们以几种方式使用“所有”这个词，这些方式由推理的思维过程定义。

无伴奏阿喀琉斯奏鸣曲

这是一个非常有趣的故事。

道格拉斯提出了一个同构的字谜。

一个单词，其中字母‘A’, ‘D’, ‘A’, ‘C’连续出现。

一个以“HE”开头并以“HE”结尾的单词。

答案是头痛。

中文版的谜题也非常巧妙。

一个词语，其中两个部首依次是“昔”和“火”。

一个词语，以部首“虫”开头，以部首“虫”结尾。

答案是“蜡烛”，意为蜡烛。